Theorems of Boolean Algebra
Theorems of Boolean Algebra
The theorems of Boolean algebra can be used to simplify many complex Boolean expression and also to transform the given expression into a more useful and meaningful equivalent expression. These theorems are discussed as below.
1 Complementation Laws
The term complement implies to invert, i.e. to change 1’s to 0’s and 0’s to 1’s. The five laws of complementation are as follows:
1. The complement of 0 is 1, i.e. Ō = 1
2. The complement of 1 is 0, i.e. Ī = 0
3. If A = 0, then Ā = 1
4. If A = 1, then Ā = 0
5. The double complementation does not change the function, i.e.
2 AND Laws
The four AND laws are as follows:
3 OR Laws
The four OR laws are as follows:
4 Commutative Laws
Commutative law states that the order of the variable in OR and AND operations is not important. The two commutative laws are
A + B = B + A
A * B = B * A
5 Associative Laws
Associative law states that the grouping of variables in AND or OR expression does not affect the result. There are two associative laws.
A +(B + C) = (A + B)+ C
A * (B * C) = (A * B) * C
6 Distributive Law
The distributive laws allow factoring or multiplying out of expressions. There are two distributive laws
A(B + C) = AB + AC
A + BC = (A + B)(A + C)
7 Redundant Literal Rule
This law states that ORing of a variable with the AND of the complement of that variable with another variable, is equal to ORing of the two variables, i.e.
A + ĀB = A + B
Another theorem based on this law is
A(Ā+ B) = AB
8 Idempotent Law
Idempotence means the same value. There are two idempotent laws
A : A : A :g: A = A
A + A + A +g+ A = A
9 Absorption Law
There are two absorption laws
A + A : B = A
A : _A + Bi = A
10 Consensus Theorem
There are two consensus theorems,
11 Transposition Theorem
There are two transposition theorems, the first is given as
12 De Morgan’s Theorem
De Morgan’s theorem gives two of the most powerful laws in Boolean algebra. These theorems are very useful in simplification of Boolean expressions,
13 Shannon’s Expansion Theorem
According to this theorem, any switching expression can be decomposed with respect to a variable A into two parts, one containing A and the other containing A. This concept is useful in decomposing complex system into an interconnection of smaller components.
f (A,B,C, ....) = A * f (1,B,C...)+ Ā * f (0,B,C, ...)
f (A,B,C, ...) = [A + f(0,B,C, ...)]*[ Ā+ f (1,B,C, ...)]
SIMPLIFICATION OF BOOLEAN EXPRESSIONS USING BOOLEAN ALGEBRA
In Boolean algebra, we have to reduce the Boolean expression into its simplest form such that the hardware cost reduces efficiently. The basic rules, laws and theorems of Boolean algebra discussed in this chapter, are used to simplify Boolean expressions. The following steps are used to simplify a Boolean expression using Boolean algebra,
METHODOLOGY: TO SIMPLIFY A BOOLEAN EXPRESSION USING BOOLEAN ALGEBRA
- Remove all parentheses and multiply all variables.
- Look for the identical terms. Only one of those terms be retained and all others skipped. For example,
- Look for a variable and its complement in the same term. This term can be removed. For example,
- Look for pairs of terms that are identical except for one variable which may be missing in one of the terms. The larger term can be removed. For example,
- Look for pairs of terms which have the same variables, except in one term a variable is complemented and in other term is it not. Such terms can be combined into a single terms. For example,
- Apply Boolean theorem and laws discussed earlier for further simplification.
1 Complement of Boolean Function
The complement of a Boolean function is obtained in the following steps:
- METHODOLOGY: TO OBTAIN COMPLEMENT OF BOOLEAN EXPRESSION
- Change all the ANDs to ORs and all the ORs to ANDs i.e., change all ‘:’ to ‘+’ and all ‘+’ to ‘:’
- Complement each of the individual variables.
- Change all 0’s to 1’s and 1’s to 0’s.
2 Principal of Duality
Duality is a very important property of Boolean algebra. The dual of a Boolean expression is obtained by replacing all ‘:’ operations with ‘+’ operations, all ‘+’ operations with ‘:’ operations, and complementing all 0’s and 1’s. The variables are not complemented in this process. Dual of a function f (A,B,C, ...) is given as
3 Relation Between Complement and Dual
For a given Boolean expression f _A,B,C, ...i the relation between its complement and dual expressions are given as
where subscript ‘c ’ represents the complement and subscript ‘d ’ represents the dual of the given function.
NOTE :
The above relation states that the dual can be obtained by complementing all the literals in complement function
REFERENCES











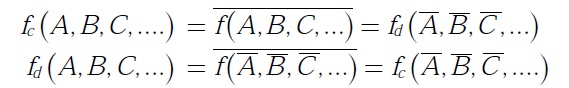


Comments
Post a Comment