5 variable K-Map in Digital Logic

Karnaugh Map or K-Map is an alternative way to write truth table and is used for the simplification of Boolean Expressions. So far we are familiar with 3 variable K-Map & 4 variable K-Map. Now, let us discuss the 5-variable K-Map in detail.

Any Boolean Expression or Function comprising of 5 variables can be solved using the 5 variable K-Map. Such a 5 variable K-Map must contain $2^{5}$ = 32 cells. Let the 5-variable Boolean function be represented as :

f ( P Q R S T) where P, Q, R, S, T are the variables and P is the most significant bit variable and T is the least significant bit variable.

The structure of such a K-Map for SOP expression is given below :

The cell no. written corresponding to each cell can be understood from the example described here:

Here for variable P=0, we have Q = 0, R = 1, S = 1, T = 1 i.e. (PQRST)=(00111) . In decimal form, this is equivalent to 7. So, for the cell shown above the corresponding cell no. = 7. In a similar manner, we can write cell numbers corresponding to every cell as shown in the above figure.
Now let us discuss how to use a 5 variable K-Map to minimize a Boolean Function.

Rules to be followed :

If a function is given in compact canonical SOP(Sum of Products) form then we write “1” corresponding to each minterm ( provided in the question ) in the corresponding cell numbers. For eg:
For $\sum\ m(0, 1, 5, 7, 30, 31)$ we will write “1” corresponding to cell numbers (0, 1, 5, 7, 30 and 31).
If a function is given in compact canonical POS(Product of Sums) form then we write “0” corresponding to each maxterm ( provided in the question ) in the corresponding cell numbers. For eg:
For $\prod\ M(0, 1, 5, 7, 30, 31)$ we will write “0” corresponding to cell numbers (0, 1, 5, 7, 30 and 31).

Steps to be followed :

Make the largest possible size subcube covering all the marked 1’s in case of SOP or all marked 0’s in case of POS in the K-Map. It is important to note that each subcube can only contain terms in powers of 2 . Also a subcube of $2^{m}$ cells is possible if and only if in that subcube for every cell we satisfy that “m” number of cells are adjacent cells .
All Essential Prime Implicants (EPIs) must be present in the minimal expressions.

I. Solving SOP function –
For clear understanding, let us solve the example of SOP function minimization of 5 Variable K-Map using the following expression :
$\sum\ m(0, 2, 4, 7, 8, 10, 12, 16, 18, 20, 23, 24, 25, 26, 27, 28)$

In the above K-Map we have 4 subcubes:

Subcube 1: The one marked in red comprises of cells ( 0, 4, 8, 12, 16, 20, 24, 28)
Subcube 2: The one marked in blue comprises of cells (7, 23)
Subcube 3: The one marked in pink comprises of cells ( 0, 2, 8, 10, 16, 18, 24, 26)
Subcube 4: The one marked in yellow comprises of cells (24, 25, 26, 27)

Now, while writing the minimal expression of each of the subcubes we will search for the literal that is common to all the cells present in that subcube.

Subcube 1: $\bar S$ $\bar T$
Subcube 2: $\bar Q$ $R$ $S$ $T$
Subcube 3: $\bar R$ $\bar T$
Subcube 4: $P$ $Q$ $\bar R$

Finally the minimal expression of the given boolean Function can be expressed as follows :
$f(P Q R S T) = \bar S$ $\bar T$ $+ \bar Q$ $R$ $S$ $T$ $+ \bar R$ $\bar T$ $+ P$ $Q$ $\bar R$

II. Solving POS function –
Now, let us solve the example of POS function minimization of 5 Variable K-Map using the following expression :
$\prod\ M(0, 2, 4, 7, 8, 10, 12, 16, 18, 20, 23, 24, 25, 26, 27, 28)$

In the above K-Map we have 4 subcubes:

Subcube 1: The one marked in red comprises of cells ( 0, 4, 8, 12, 16, 20, 24, 28)
Subcube 2: The one marked in blue comprises of cells (7, 23)
Subcube 3: The one marked in pink comprises of cells ( 0, 2, 8, 10, 16, 18, 24, 26)
Subcube 4: The one marked in yellow comprises of cells (24, 25, 26, 27)

Now, while writing the minimal expression of each of the subcubes we will search for the literal that is common to all the cells present in that subcube.

Subcube 1: $S + T$
Subcube 2: $Q + \bar R$ $+ \bar S$ $+ \bar T$
Subcube 3: $R + T$
Subcube 4: $\bar P + \bar Q$ $+ R$

Finally the minimal expression of the given boolean Function can be expressed as follows :
$f(P Q R S T) = (S + T)(Q + \bar R + \bar S + \bar T)( R + T)(\bar P + \bar Q + R)$

NOTE:

For the 5 variable K-Map, the Range of the cell numbers will be from 0 to $2^{5}$ -1 i.e. 0 to 31.
The above mentioned term “Adjacent Cells” means that “any two cells which differ in only 1 variable”.

Variable Entrant Map (VEM) in Digital Logic

K-map is the best manual technique to solve Boolean equations, but it becomes difficult to manage when number of variables exceed 5 or 6. So, a technique called Variable Entrant Map (VEM) is used to increase the effective size of k-map. It allows a smaller map to handle large number of variables. This is done by writing output in terms of input.

Example – A 3-variable function can be defined as a function of 2-variables if the output is written in terms of third variable.

Consider a function F(A,B,C) = (0,1,2,5)

If we define F in terms of ‘C’, then this function can be written as:

And the VEM for this is:

Advantages of using VEM –

A VEM can be used to plot more than ‘n’ variables using an ‘n’ variable K-map.
It is commonly used to solve problems involving multiplexers.

Minimization procedure for VEM – Now, let’s see how to find SOP expression if a VEM is given.

Write all the variables(original and complimented forms are treated as two different variables) in the map as 0, leave 0’s, minterms and don’t cares as it is and obtain the SOP expression.
(a) Select one variable and make all occurrences of that variable as 1, write minterms (1’s) as don’t cares, leave 0’s and don’t cares as it is. Now, obtain the SOP expression.
(b) Multiply the obtained SOP expression with the concerned variable.
Repeat step 2 for all the variables in the k-map.
SOP of VEM is obtained by ORing all the obtained SOP expressions.
Let’s apply the above procedure on a sample VEM (X is used to represent don’t care):

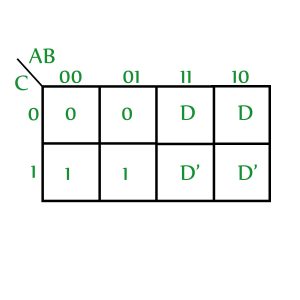
Step 1: Write all the variables as 0 (D and D’ are considered as two different variables), leave minterms, 0’s and don’t cares as it is and obtain the SOP expression.

 SOP obtained: A'C

Step 2:
(a) Replace all occurrences of D with 1, all occurrences of D’ with 0 and all 1’s with don’t care. Leave 0’s and don’t cares as it is.

(b) Multiply the obtained SOP with the concerned variable.

SOP obtained: AC'D

Step 3: Repeat step 2 for D’

(a) Replace all occurrences of D’ with 1, all occurrences of D with 0 and all 1’s with don’t care. Leave 0’s and don’t cares as it is.

(b) Multiply the obtained SOP with the concerned variable.

SOP obtained: CD'

Step 4: SOP of VEM is obtained by ORing all the obtained SOP expressions. Therefore, the SOP expression for the given VEM is: A'C + AC'D + CD'

Minimization of Boolean Functions
As discussed in the “Representation of Boolean Functions” every boolean function can be expressed as a sum of minterms or a product of maxterms. Since the number of literals in such an expression is usually high, and the complexity of the digital logic gates that implement a Boolean function is directly related to the complexity of the algebraic expression from which the function is implemented, it is preferable to have the most simplified form of the algebraic expression.
The process of simplifying the algebraic expression of a boolean function is called minimization. Minimization is important since it reduces the cost and complexity of the associated circuit.
For example, the function  can be minimized to . The circuits associated with above expressions is –
It is clear from the above image that the minimized version of the expression takes a less number of logic gates and also reduces the complexity of the circuit substantially. Minimization is hence important to find the most economic equivalent representation of a boolean function.
Minimization can be done using Algebraic Manipulation or K-Map method. Each method has it’s own merits and demerits.
Minimization using Algebraic Manipulation –
This method is the simplest of all methods used for minimization. It is suitable for medium sized expressions involving 4 or 5 variables. Algebraic manipulation is a manual method, hence it is prone to human error.
Common Laws used in algebraic manipulation :
Example 1 – Minimize the following boolean function using algebraic manipulation-
Solution – Properties refer to the three common laws mentioned above.
Minimization using K-Map –
The Algebraic manipulation method is tedious and cumbersome. The K-Map method is faster and can be used to solve boolean functions of upto 5 variables. Please refer this link to learn more about K-Map.
Example 2 – Consider the same expression from example-1 and minimize it using K-Map.
Solution – The following is a 4 variable K-Map of the given expression.

The above figure highlights the prime implicants in green, red and blue.
The green one spans the whole third row, which gives us – 
The red one spans 4 squares, which gives us – 
The blue one spans 4 squares, which gives us – 
So, the minimized boolean expression is- 
Consensus Theorem in Digital Logic
Redundancy theorem is used as a Boolean algebra trick in Digital Electronics. It is also known as Consensus Theorem:
AB + A'C + BC = AB + A'C
The consensus or resolvent of the terms AB and A’C is BC. It is the conjunction of all the unique literals of the terms, excluding the literal that appears unnegated in one term and negated in the other.
The conjunctive dual of this equation is:
(A+B).(A'+C).(B+C) = (A+B).(A'+C)
In the second line, we omit the third product term BC.Here, the term BC is known as Redundant term. In this way we use this theorem to simply the Boolean Algebra. Conditions for applying Redundancy theorem are:
Three variables must present in the expression.Here A, B and C are used as variables.
Each variables is repeated twice.
One variable must present in complemented form.
After applying this theorem we can only take those terms which contains the complemented variable.
Proof – We can also prove it like this:
Y = AB + A'C + BC
Y = AB + A'C + BC.1
Y = AB + A'C + BC.(A + A')
Y = AB + A'C + ABC + A'BC
Y = AB(1 + C) + A'C(1 + B)
Y = AB + A'C             
Example-1.
F = AB + BC' + AC
Here, we have three variables A, B and C and all are repeated twice. The variable C is present in complemented form. So, all the conditions are satisfied for applying this theorem.
After applying Redundancy theorem we can write only the terms containing complemented variables (i.e, C) and omit the Redundancy term i.e., AB.
 .'. F = BC' + AC
Example-2.
F = (A + B).(A' + C).(B + C)
Three variables are present and all are repeated twice. The variable A is present in complemented form.Thus, all the three conditions of this theorem is satisfied.
After applying Redundancy theorem we can write only the terms containing complemented variables (i.e, A) and omit the Redundancy term i.e., (B + C).
.'. F = (A + B).(A' + C)
Consider the following equation:
Y = AB + A'C + BC
The third product term BC is a redundant consensus term. If A switches from 1 to 0 while B=1 and C=1, Y remains 1. During the transition of signal A in logic gates, both the first and second term may be 0 momentarily. The third term prevents a glitch since its value of 1 in this case is not affected by the transition of signal A.
Thus. it is important to remove Logic Redundancy because it causes unnecessary network complexity and raises the cost of implementation.
So, in this way we can minimize a Boolean expression to solve it.