Introduction of K-Map (Karnaugh Map)
In many digital circuits and practical problems we need to find expression with minimum variables. We can minimize Boolean expressions of 3, 4 variables very easily using K-map without using any Boolean algebra theorems. K-map can take two forms Sum of Product (SOP) and Product of Sum (POS) according to the need of problem. K-map is table like representation but it gives more information than TRUTH TABLE. We fill grid of K-map with 0’s and 1’s then solve it by making groups.
Steps to solve expression using K-map-
- Select K-map according to the number of variables.
- Identify minterms or maxterms as given in problem.
- For SOP put 1’s in blocks of K-map respective to the minterms (0’s elsewhere).
- For POS put 0’s in blocks of K-map respective to the maxterms(1’s elsewhere).
- Make rectangular groups containing total terms in power of two like 2,4,8 ..(except 1) and try to cover as many elements as you can in one group.
- From the groups made in step 5 find the product terms and sum them up for SOP form.
SOP FORM :1. K-map of 3 variables –
Z= ∑A,B,C(1,3,6,7)
From red group we get product term— A’C
From green group we get product term— AB
Summing these product terms we get- Final expression (A’C+AB)
2. K-map for 4 variables –
F(P,Q,R,S)=∑(0,2,5,7,8,10,13,15) 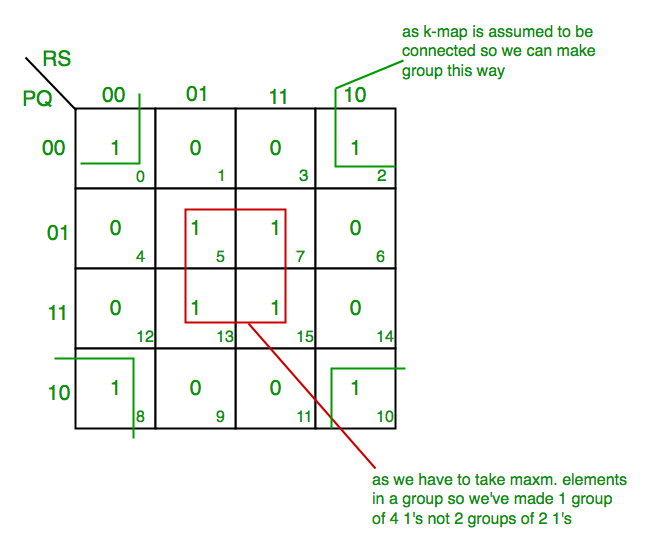
From red group we get product term— QS
From green group we get product term— Q’S’
Summing these product terms we get- Final expression (QS+Q’S’)
POS FORM :
1. K-map of 3 variables –
F(A,B,C)=π(0,3,6,7)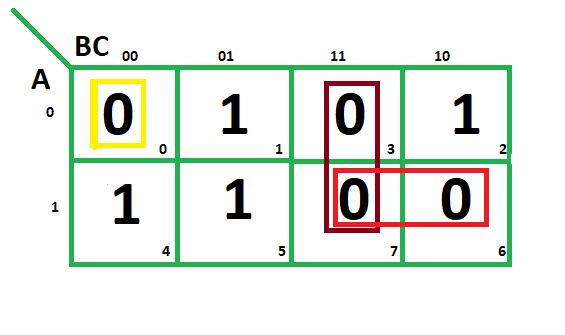
From red group we find terms - A B
Taking complement of these two - A' B'
Now sum up them - (A' + B')
From brown group we find terms - B C
Taking complement of these two terms - B’ C’
Now sum up them - (B’+C’)
From yellow group we find terms - A' B' C’
Taking complement of these two - A B C
Now sum up them - (A + B + C)
We will take product of these three terms : Final expression –
(A' + B’) (B’ + C’) (A + B + C)
2. K-map of 4 variables –
F(A,B,C,D)=π(3,5,7,8,10,11,12,13)
From green group we find terms - C’ D B
Taking their complement and summing them -(C+D’+B’)
From red group we find terms - C D A’
Taking their complement and summing them - (C’+D’+A)
From blue group we find terms- A C’ D’
Taking their complement and summing them -(A’+C+D)
From brown group we find terms- A B’ C
Taking their complement and summing them -(A’+B+C’)
Finally we express these as product –(C+D’+B’).(C’+D’+A).(A’+C+D).(A’+B+C’)
PITFALL– *Always remember POS ≠ (SOP)’
*The correct form is (POS of F)=(SOP of F’)’
Various Implicants in K-Map
Implicant is a product/minterm term in Sum of Products (SOP) or sum/maxterm term in Product of Sums (POS) of a Boolean function. E.g., consider a boolean function, F = AB + ABC + BC. Implicants are AB, ABC and BC.
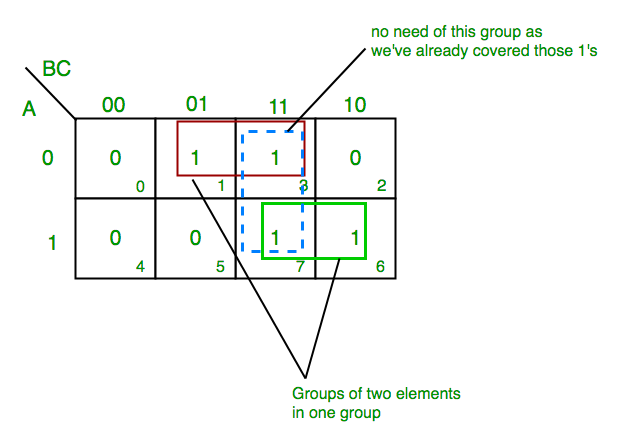
1. Prime Implicants –A group of square or rectangle made up of bunch of adjacent minterms which is allowed by definition of K-Map are called prime implicants(PI) i.e. all possible groups formed in K-Map. Example:

2. Essential Prime Implicants – These are those subcubes(groups) which cover atleast one minterm that can’t be covered by any other prime implicant. Essential prime implicants(EPI) are those prime implicants which always appear in final solution.
Example:
3. Redundant Prime Implicants – The prime implicants for which each of its minterm is covered by some essential prime implicant are redundant prime implicants(RPI). This prime implicant never appears in final solution. Example:

4. Selective Prime Implicants- The prime implicants for which are neither essential nor redundant prime implicants are called selective prime implicants(SPI). These are also known as non-essential prime implicants. They may appear in some solution or may not appear in some solution.
Example:
Example-1: Given F = ∑(1, 5, 6, 7, 11, 12, 13, 15), find number of implicant, PI, EPI, RPI and SPI.
 No. of Implicants = 8
No. of Implicants = 8
No. of Prime Implicants(PI) = 5
No. of Essential Prime Implicants(EPI) = 4
No. of Redundant Prime Implicants(RPI) = 1
No. of Selective Prime Implicants(SPI) = 0
Example-2: Given F = ∑(0, 1, 5, 8, 12, 13), find number of implicant, PI, EPI, RPI and SPI.

No. of Implicants = 6
No. of Prime Implicants(PI) = 6
No. of Essential Prime Implicants(EPI) = 0
No. of Redundant Prime Implicants(RPI) = 0
No. of Selective Prime Implicants(SPI) = 6
Example-3: Given F = ∑(0, 1, 5, 7, 15, 14, 10), find number of implicant, PI, EPI, RPI and SPI.

No. of Implicants = 7
No. of Prime Implicants(PI) = 6
No. of Essential Prime Implicants(EPI) = 2
No. of Redundant Prime Implicants(RPI) = 2
No. of Selective Prime Implicants(SPI) = 4

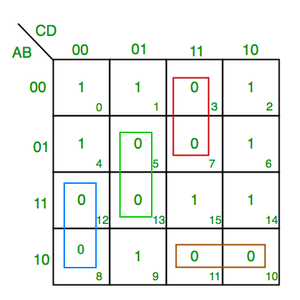




 No. of Implicants = 8
No. of Implicants = 8




Comments
Post a Comment