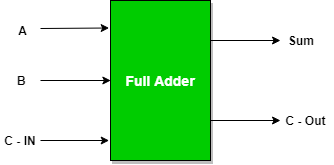
Full Adder

Full Adder is the adder which adds three inputs and produces two outputs. The first two inputs are A and B and the third input is an input carry as C-IN. The output carry is designated as C-OUT and the normal output is designated as S which is SUM.

A full adder logic is designed in such a manner that can take eight inputs together to create a byte-wide adder and cascade the carry bit from one adder to another.

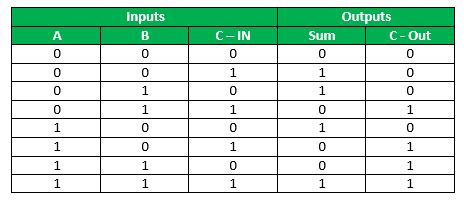
Full Adder Truth Table:

The SOP form can be obtained with the help of K-map as:

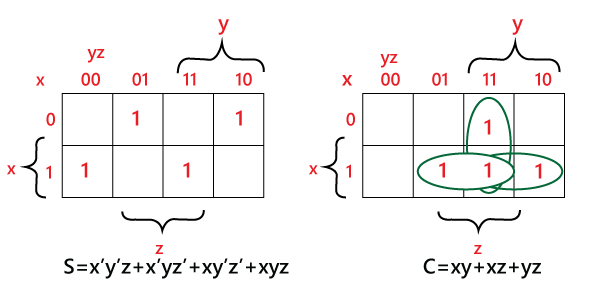
Full Adder

Sum = x' y' z+x' yz+xy' z'+xyz
Carry = xy+xz+yz

Logical Expression for SUM:
= A’ B’ C-IN + A’ B C-IN’ + A B’ C-IN’ + A B C-IN
= C-IN (A’ B’ + A B) + C-IN’ (A’ B + A B’)
= C-IN XOR (A XOR B)
= (1,2,4,7)

Logical Expression for C-OUT:
= A’ B C-IN + A B’ C-IN + A B C-IN’ + A B C-IN
= A B + B C-IN + A C-IN
= (3,5,6,7)

Another form in which C-OUT can be implemented:
= A B + A C-IN + B C-IN (A + A’)
= A B C-IN + A B + A C-IN + A’ B C-IN
= A B (1 +C-IN) + A C-IN + A’ B C-IN
= A B + A C-IN + A’ B C-IN
= A B + A C-IN (B + B’) + A’ B C-IN
= A B C-IN + A B + A B’ C-IN + A’ B C-IN
= A B (C-IN + 1) + A B’ C-IN + A’ B C-IN
= A B + A B’ C-IN + A’ B C-IN
= AB + C-IN (A’ B + A B’)
Therefore COUT = AB + C-IN (A EX–OR B)

Full Adder logic circuit.

Implementation of Full Adder using Half Adders
2 Half Adders and an OR gate are required to implement a Full Adder.

With this logic circuit, two bits can be added together, taking a carry from the next lower order of magnitude, and sending a carry to the next higher order of magnitude.

Implementation of Full Adder using NAND gates:

Implementation of Full Adder using NOR gates:
Total 9 NOR gates are required to implement a Full Adder.

Sum:

  • Perform the XOR operation of inputs A and B.
  • Perform the XOR operation of the outcome with carry. So, the sum is (A XOR B) XOR Cin which is also represented as:
    (A ⊕ B) ⊕ Cin

Carry:

  1. Perform the 'AND' operation of input A and B.
  2. Perform the 'XOR' operation of input A and B.
  3. Perform the 'OR' operations of both the outputs that come from the previous two steps. So the 'Carry' can be represented as:
    A.B + (A ⊕ B)

Comments

Post a Comment

Popular posts from this blog

Introduction of K-Map (Karnaugh Map) Part 2

Image
  5 variable K-Map in Digital Logic Karnaugh Map  or K-Map is an alternative way to write truth table and is used for the simplification of Boolean Expressions. So far we are familiar with 3 variable K-Map & 4 variable K-Map. Now, let us discuss the 5-variable K-Map in detail. Any Boolean Expression or Function comprising of 5 variables can be solved using the 5 variable K-Map. Such a 5 variable K-Map must contain   = 32 cells . Let the 5-variable Boolean function be represented as : f ( P Q R S T)  where P, Q, R, S, T are the variables and P is the most significant bit variable and T is the least significant bit variable. The structure of such a K-Map for SOP expression is given below : The cell no. written corresponding to each cell can be understood from the example described here: Here for variable  P=0, we have Q = 0, R = 1, S = 1, T = 1 i.e. (PQRST)=(00111)  . In decimal form, this is equivalent to  7 . So, for the cell shown above the c...
Read more

Alternate Logic-Gate Representations

Image
Alternate Logic-Gate Representations We have discussed the five basic logic gates (AND, OR, INVERTER, NAND, and NOR) and the standard symbols used to represent them in a logic circuit diagram. Most of the logic networks use standard symbols. But in some networks an alternative set of symbols is used in addition to the standard symbols. The table shows the alternate set of symbols for the five basic gates. Table: Alternate Logic Gate Representations To convert any normal symbol to its corresponding alternate symbol, the following steps are used: METHODOLOGY: TO CONVERT STANDARD SYMBOL TO ALTERNATE SYMBOL Step 1: Add bubbles (indication of inversion) at those input or output points where it is not present. Step 2: Remove all pre-existing bubbles of the normal symbol, if there is any at the point (only NOT, NAND and NOR gates) Step 3: If the existing normal logic symbol is AND, change it to OR, Similarly, if it is OR, then change it to AND. There is no change for the triangular symbol of ...
Read more

Number Systems

Image
  Table: - Various number systems and their bases S. No Name of Number System Base/Radix 1. Binary 2 2. Octal 8 3. Decimal 10 4. Hexadecimal 16 Table: - number systems S. No Name of Number System Base/Radix First Digit Last Digit All Digits/ Characters 1. Binary 2 0 1 0,1 2. Octal 8 0 7 0,1,2,3,4,5,6,7 3. Decimal 10 0 9 0,1,2,3,4,5,6,7,8,9 4. Hexadecimal 16 0 F 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F Table: - Number Formats S. No Name Size (bits) Example 1. Bit 1 1 2. Nibble 4 1010 3. Byte 8 1000 1100 4. Word 16 1010 1010 1010 1010 5. Double Word 32 1100 1100 1100 1100 1100 1100 1100 1100 Table: - Decimal, Binary, Octal and Hexadecimal Number S. No Decimal Binary Octal Hexadecimal 1. 0 0000 0 0 2. 1 0001 1 1 3. 2 0010 2 2 4. 3 0011 3 3 5. 4 0100 4 4 6. 5 0101 5 5 7. 6 0110 6 6 8. 7 0111 7 7 9. 8 1000 10 8 10. 9 1001 11 9 11. 10 1010 12 A 12. 11 1011 13 B 13. 12 1100 14 C 14. 13 1101 15 D 15. 14 1110 16 E 16. 15 1111 17 F 17. 16 0001 0000 20 10 18. 17 0001 0001 21 11 19. 18 0001 0010 22 12 ...
Read more